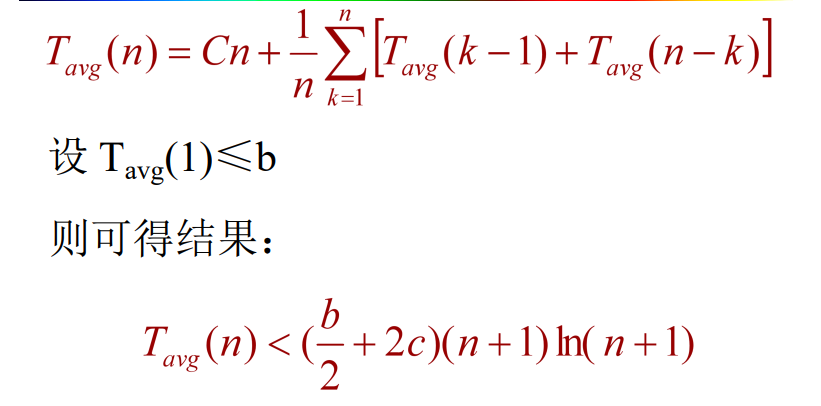希尔排序 希尔(shell)排序是插入排序的一种。也称缩小增量排序 ,是直接插入排序的一种更高效的改进版本。希尔排序是非稳定排序。希尔排序是按照记录下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量减少,每组包含的关键词增多,当增量减少至1时,所有元素被分为1组,算法结束。跳跃分割 的策略:将相距某个“增量”的记录组成一个子序列,这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 template <typename E>void inssort (E A[],int n,int incr) for (int i = incr;i < n;i += incr){ for (int j = i;(j > incr) && (A[j] < A[j-incr]);j -= incr) swap (A,j,j - incr); } } template <typename E>void shellsort (E A[],int n) for (int i = n/2 ;i > 2 ;i /= 2 ) for (int j = 0 ;j < i;j ++) inssort <E>(A[j],n-j,j); inssort <E,Comp>(A,n,1 ); }
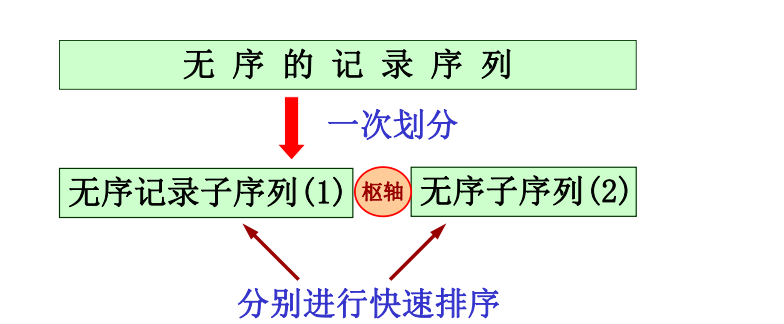
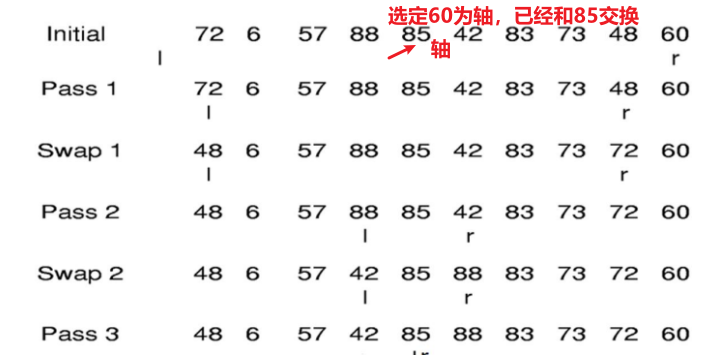
快速排序 一趟快速排序思想 枢轴 ,凡其关键字小于枢轴的记录均移动至该记录之前,反之,凡关键字大于枢轴的记录均移动至该记录之后。致使一趟排序之后,记录的无序序列A[s..t]将分割成两部分:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 template <typename E>inline int findpivot (E A[],int i,int j) return (i+j)/2 ; }template <typename E>int partition (E A[],int l,int r,E& pivot) do { while (A[++l] < pivot); while ((l < r) && A[--r] > pivot); swap (A,l,r); }while (l < r) return l; } template <typename E>void qsort (E A[],int i,int j) if (j <= i)return ; int pivotindex = findpivot (A,i,j); swap (A,pivotindex,j); int k = partition <E>(A,i-1 ,j,A[j]); swap (A,k,j); qsort <E>(A,i,k-1 ); qsort <E>(A,k+1 ,j); }
5、时间复杂度结论 :
合并(归并)排序 算法思想:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 template <tyepname E>void merge (E A[],E temp[],int left,int right) if (left == right) return ; int mid = (left+right)/2 ; mergesort <E>(A,temp,left,mid); mergesort <E>(A,temp,mid+1 ,right); for (int i = left;i <= right;i ++) temp[i] = A[i]; int i1 = left,i2 = mid + 1 ; for (int curr = left; curr <= right;curr ++){ if (i1 == mid + 1 ) A[curr] = temp[i2++]; else if (i2 > right) A[curr] = temp[i1++]; else if (temp[i1] < temp[i2]) A[curr] = temp[i1++]; else A[curr] = temp[i2++]; } }
时间复杂度:O(nlogn)